高考天津市理科数学真题下载

今天小编为大家整理了有关于高考天津市理科数学真题，希望可以对大家有帮助。

高考天津市理科数学真题

一、选择题

1．已知全集，集合，集合，则集合（ ）

A． B． C． D．

2．设变量满足约束条件则目标函数的最大值为（ ）

A． B． C． D．

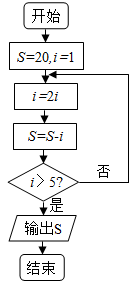
3．阅读下边的程序框图，运行相应的程序，则输出的值为（ ）

A． B． C． D．

4．设，则“”是“”的（ ）

A．充分而不必要条件 B．必要而不充分条件

C．充要条件 D．既不充分也不必要条件

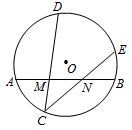5．如图，在圆中，是弦的三等分点，弦，分别经过点，若，，，则线段的长为（ ）

A． B．3 C． D．

6．已知双曲线（）的一条渐近线过点（），且双曲线的一个焦点在抛物线的准线上，则双曲线的方程为（ ）

A． B． C． D．

7．已知定义在上的函数（为实数）为偶函数，记，，，则的大小关系为（ ）

A． B． C． D．

8．已知函数函数，其中，若函数恰有个零点，则的取值范围是（ ）

A． B． C． D．

二、填空题

9．是虚数单位，若复数是纯虚数，则实数的值为 ．

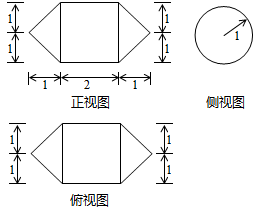
10．一个几何体的三视图如图所示（单位：m），则该几何体的体积为 ．

11．曲线与直线所围成的封闭图形的面积为 ．

12．在的展开式中，的系数为 ．

13．在中，内角所对的边分别为.已知的面积为，，则的值为 ．

14．在等腰梯形中，已知。动点和分别在线段和上，且，则的最小值为 ．

三、解答题

15．已知函数，．

（Ⅰ）求的最小正周期；

（Ⅱ）求在区间内的最大值和最小值．

16．为推动乒乓球运动的发展，某乒乓球比赛允许不同协会的运动员组队参加。现有来自甲协会的运动员名，其中种子选手名；乙协会的运动员名，其中种子选手名。从这名运动员中随机选择人参加比赛。

（Ⅰ）设为事件“选出的人中恰有名种子选手，且这名种子选手来自同一个协会”，求事件发生的概率；

（Ⅱ）设为选出的人中种子选手的人数，求随机变量的分布列和数学期望．

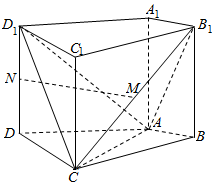17．如图，在四棱柱中，侧棱底面，，，，，且点和分别为和的中点．

（Ⅰ）求证：平面；

（Ⅱ）求二面角的正弦值；

（Ⅲ）设为棱上的点。若直线和平面所成角的正弦值为，求线段的长。

18．已知数列满足（为实数，且），，，，且，，成等差数列。

（Ⅰ）求的值和 的通项公式；

（Ⅱ）设，，求数列的前项和．

19．已知椭圆的左焦点为，离心率为，点在椭圆上且位于第一象限，直线被圆截得的线段的长为，．

（Ⅰ）求直线的斜率；

（Ⅱ）求椭圆的方程；

（Ⅲ）设动点在椭圆上，若直线的斜率大于，求直线（为原点）的斜率的取值范围。

20．已知函数其中，且.

（Ⅰ）讨论的单调性；

（Ⅱ）设曲线与轴正半轴的交点为，曲线在点处的切线方程为，

求证：对于任意的正实数，都有；

（Ⅲ）若关于的方程（为实数）有两个正实数根，求证：．

高考天津市理科数学真题答案

一、选择题

1．答案：A

解析过程：

,所以，选A

2．答案：C

解析过程：

不等式所表示的平面区域如下图所示，

当所表示直线经过点时，有最大值，选C

3．答案：B

解析过程：

输入；

不成立；

不成立

成立

输出,选B

4．答案：A

解析过程：

，

所以“”是“”的充分不必要条件，选A

5．答案：A

解析过程：

由相交弦定理可知，

，

又因为是弦的三等分点，

所以，

所以，选A

6．答案：D

解析过程：

双曲线（）的渐近线方程为，

由点在渐近线上，所以，

双曲线的一个焦点在抛物线准线方程上，

所以，由此可解得，

所以双曲线方程为，选D

7．答案：C

解析过程：

因为函数为偶函数，所以，即，

所以

所以，选C

8．答案：D

解析过程：

由得，

所以，

即

,

所以恰有4个零点等价于方程

有4个不同的解，

即函数与函数的图象的4个公共点，

由图象可知.选D

二、填空题

9．答案：-2

解析过程：

是纯虚数，

所以，即

10．答案：

解析过程：

由三视图可知，该几何体是中间为一个底面半径为，

高为的圆柱，两端是底面半径为，高为的圆锥，

所以该几何体的体积.

11．答案：

解析过程：

两曲线的交点坐标为，

所以它们所围成的封闭图形的面积

.

12．答案：

解析过程：

今天小编为大家整理了有关于高考天津市理科数学真题，希望可以对大家有帮助。

高考天津市理科数学真题

一、选择题

1．已知全集，集合，集合，则集合（ ）

A． B． C． D．

2．设变量满足约束条件则目标函数的最大值为（ ）

A． B． C． D．

3．阅读下边的程序框图，运行相应的程序，则输出的值为（ ）

A． B． C． D．

4．设，则“”是“”的（ ）

A．充分而不必要条件 B．必要而不充分条件

C．充要条件 D．既不充分也不必要条件

5．如图，在圆中，是弦的三等分点，弦，分别经过点，若，，，则线段的长为（ ）

A． B．3 C． D．

6．已知双曲线（）的一条渐近线过点（），且双曲线的一个焦点在抛物线的准线上，则双曲线的方程为（ ）

A． B． C． D．

7．已知定义在上的函数（为实数）为偶函数，记，，，则的大小关系为（ ）

A． B． C． D．

8．已知函数函数，其中，若函数恰有个零点，则的取值范围是（ ）

A． B． C． D．

二、填空题

9．是虚数单位，若复数是纯虚数，则实数的值为 ．

10．一个几何体的三视图如图所示（单位：m），则该几何体的体积为 ．

11．曲线与直线所围成的封闭图形的面积为 ．

12．在的展开式中，的系数为 ．

13．在中，内角所对的边分别为.已知的面积为，，则的值为 ．

14．在等腰梯形中，已知。动点和分别在线段和上，且，则的最小值为 ．

三、解答题

15．已知函数，．

（Ⅰ）求的最小正周期；

（Ⅱ）求在区间内的最大值和最小值．

16．为推动乒乓球运动的发展，某乒乓球比赛允许不同协会的运动员组队参加。现有来自甲协会的运动员名，其中种子选手名；乙协会的运动员名，其中种子选手名。从这名运动员中随机选择人参加比赛。

（Ⅰ）设为事件“选出的人中恰有名种子选手，且这名种子选手来自同一个协会”，求事件发生的概率；

（Ⅱ）设为选出的人中种子选手的人数，求随机变量的分布列和数学期望．

17．如图，在四棱柱中，侧棱底面，，，，，且点和分别为和的中点．

（Ⅰ）求证：平面；

（Ⅱ）求二面角的正弦值；

（Ⅲ）设为棱上的点。若直线和平面所成角的正弦值为，求线段的长。

18．已知数列满足（为实数，且），，，，且，，成等差数列。

（Ⅰ）求的值和 的通项公式；